SammysHP

Seit einigen Monaten bin ich süchtig nach HP-Taschenrechnern. Für meine Masterarbeit musste ich aus den Winkeln zwischen drei Vektoren die jeweiligen Polarkoordinaten berechnen – viele Male. Ein kleines Python-Programm hätte es vermutlich getan, aber das war mir zu langweilig.

Seit vielen Jahren habe ich einen Haufen Emulatoren auf meinem Handy, u.a. TI-82, TI-83, TI-83+, TI-85, TI-86, TI-89T, HP-42S, HP 48SX und HP 48GX. Die TI-Rechner waren mir alle zu kompliziert in der Bedienung, Droid48 war mir zu hässlich und hatte einige nervige Bugs, der HP 48SX ist mir noch zu unausgereift. Der HP-42S ist zwar recht simpel, bietet aber viele Funktionen.

In diesem Artikel möchte ich einige kleine Programme vorstellen, die ich für den HP-42S (und zum Teil andere HP-Rechner) entwickelt habe.

3D-Koordinaten-Vektoren

Für die Repräsentation von dreidimensionalen Koordinaten habe ich einen Vektor der Größe drei gewählt: (x, y, z) bzw. (r, θ, φ). Hier zwei kurze Programme für die Komposition bzw. Dekomposition:

01 LBL "→V3"
02 STO "V3-A"
03 R↓
04 STO "V3-B"
05 R↓
06 STO "V3-C"
07 1
08 3
09 DIM "V3"
10 INDEX "V3"
11 1
12 1
13 STOIJ
14 RCL "V3-A"
15 STOEL
16 J+
17 RCL "V3-B"
18 STOEL
19 J+
20 RCL "V3-C"
21 STOEL
22 CLST
23 RCL "V3"

01 LBL "V3→"
02 STO "V3"
03 INDEX "V3"
04 1
05 3
06 STOIJ
07 CLST
08 RCLEL
09 J-
10 RCLEL
11 J-
12 RCLEL

Den Stack leere ich, um temporäre Elemente zu entfernen (vorherige Elemente wurden eh schon längst vom Stack gepusht). J+ wird eingegeben über XEQ "J+

Nicht ganz sicher war ich mir bei der Reihenfolge des Stacks: Soll das oberste Element x oder z beinhalten? Momentan muss man den Vektor rückwärts eingeben. Andererseits fängt man Berechnungen meistens mit der ersten Koordinate an, welche in diesem Fall ganz oben liegt.

Weiterhin bin ich mir nicht sicher, ob meine Verwendung des Stacks und der Variablen optimal ist. Ein größerer oder unendlicher Stack wie beim HP 48G wäre schön.

Nachtrag: Ich hatte die Idee, zwei Stackeinträge in einen einzigen komplexen Eintrag umzuwandeln. Dadurch passen alle Werte in den Stack und ich brauche keine benannten Variablen.

01 LBL "→V3"
02 COMPLEX
03 1
04 3
05 DIM "V3"
06 INDEX "V3"
07 R↓
08 1
09 STOIJ
10 R↓
11 R↓
12 COMPLEX
13 STOEL
14 J+
15 R↓
16 STOEL
17 J+
18 R↓
19 STOEL
20 CLST
21 RCL "V3"

Allerdings weiß ich nicht, ob sich dadurch irgendwelche Nachteile (Genauigkeit?) ergeben. Wäre toll, wenn mir jemand Tipps dazu geben könnte.

Transformation kartesische und sphärische Koordinaten

Als Eingabe wird jeweils ein wie oben definierter Vektor erwartet. Ebenso erfolgt die Rückgabe.

01 LBL "→RTP"
02 XEQ "V3→"
03 →POL
04 R↑
05 X<> ST T
06 →POL
07 XEQ "→V3"

01 LBL "→XYZ"
02 XEQ "V3→"
03 →REC
04 X<> ST T
05 R↓
06 →REC
07 XEQ "→V3"

Die Reihenfolge von θ und φ ist wie immer Geschmackssache. In diesem Fall findet die Bedeutung aus dem ISO-Standard Anwendung.

Koordinaten aus Winkeln berechnen

Nicht für den HP-42S, sondern für den HP 48 (weil ich mit ihm angefangen habe). Muss ich noch entsprechend für den HP-42S portieren.

<< -> C A B     @ assign angles to C, A and B
    <<
        C COS   @ B1 = cos(C)
        1       @ sqrt(1 - B1^2)
        OVER    @ | get B1
        SQ      @ |
        -       @ |
        SQRT    @ |
        0       @ B3 = 0
        ->V3    @ create 3D vector for B
        DUP     @ decompose copy of B
        V->     @ |
        B COS   @ C1 = cos(B)
        A COS   @ (cos(A) - B1*C1)/B2
        5 PICK  @ |
        3 PICK  @ |
        *       @ |
        -       @ |
        4 PICK  @ |
        /       @ |
        1       @ sqrt(1 - C1^2 - C2^2)
        3 PICK  @ |
        SQ      @ |
        -       @ |
        2 PICK  @ |
        SQ      @ |
        -       @ |
        SQRT    @ |
        ->V3    @ create 3D vector for C
        4 ROLLD @ delete intermediate values on stack
        3 DROPN @ |
    >>
>>

Gegeben sind die Winkel zwischen drei (unbekannten) Vektoren, gesucht werden die entsprechenden Vektoren (der Länge eins).

Nachtrag: Hier das Programm für den HP-42S:

01 LBL "BALL"
02 RCL "REGS"
03 STO "_BALLR"
04 SIZE 07
05 R↓
06 STO 00
07 R↓
08 STO 01
09 R↓
10 STO 02
11 COS
12 STO 03
13 ENTER
14 X↑2
15 1
16 X<>Y
17 -
18 SQRT
19 STO 04
20 0
21 X<> ST Z
22 XEQ "→V3"
23 STO "B"
24 RCL 01
25 COS
26 STO 05
27 ENTER
28 X↑2
29 X<>Y
30 RCL 03
31 ×
32 RCL 00
33 COS
34 X<>Y
35 -
36 RCL 04
37 ÷
38 STO 06
39 X↑2
40 +
41 1
42 X<>Y
43 -
44 SQRT
45 RCL 06
46 RCL 05
47 XEQ "→V3"
48 STO "C"
49 RCL "B"
50 RCL "_BALLR"
51 CLV "_BALLR"
52 STO "REGS"
53 CLX
54 R↓

Ich nutze zum Zwischenspeichern der Ergebnisse die Register, welche ich zuvor sichere und später wiederherstelle. Nicht perfekt, aber es funktioniert.

Free42 Skin mit großem Display

Das Skin-Paket für Free42 bietet schon einige tolle Skins. Allerdings war mir der Bildschirm immer zu klein und zu kontrastarm. Also habe ich mir selbst einen erstellt (auf Basis des Nova1-Skins):

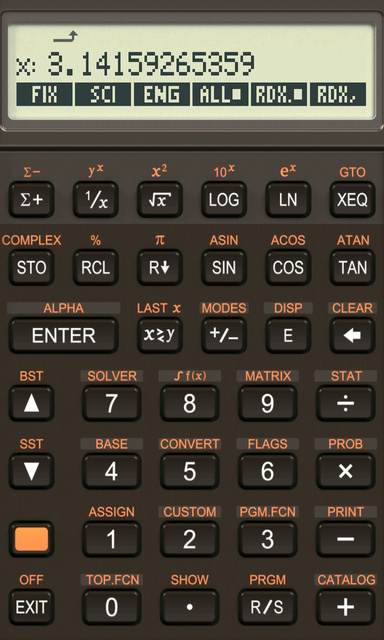
Den Skin könnt ihr euch hier herunterladen.

Eine Schlussbemerkung

Es hat nur wenige Tage gedauert und ich war HP-süchtig. Schnell wollte ich einen echten HP-Rechner haben. Aber die Preise für den 48G (!) lagen bei 50–80 €, für den 42S bei rund 200–300 €. Alles Sammlerstücke! Die Nachbauten von SwissMicros sind zwar immer noch günstiger als gebrauchte Originale, aber dennoch mit rund 100 € ziemlich teuer. Demnächst soll eine Version des HP-42S kommen, vermutlich über 200 €.